笔记

sd1. 等价无穷小

1.1. 基本无穷小

$x\to 0$	等价
$\sin x$	$x$
$\arcsin x$	$x$
$\tan x$	$x$
$\arctan x$	$x$
$e^x-1$	$x$
$\ln (1+x)$	$x$
$1-\cos x$	$\frac{1}{2}{x}^2$
$a^x-1$	$x\ln a$
$(1+x{)}^a-1$	$ax$

1.2. 拓展：反三角/三角函数的等价无穷小（泰勒展开）

泰勒展开（推导）

$$\begin{array}{rl}f(x)& =\sum _{n=0}^{\mathrm{\infty }}\frac{f^{(n)}(0)}{n!}{x}^n\\ & =f(0)+f^{\prime }(0)x+\frac{f^{″}(0)}{2!}{x}^2+\frac{f^{‴}(0)}{3!}{x}^3+\cdots \end{array}$$

几个常用的

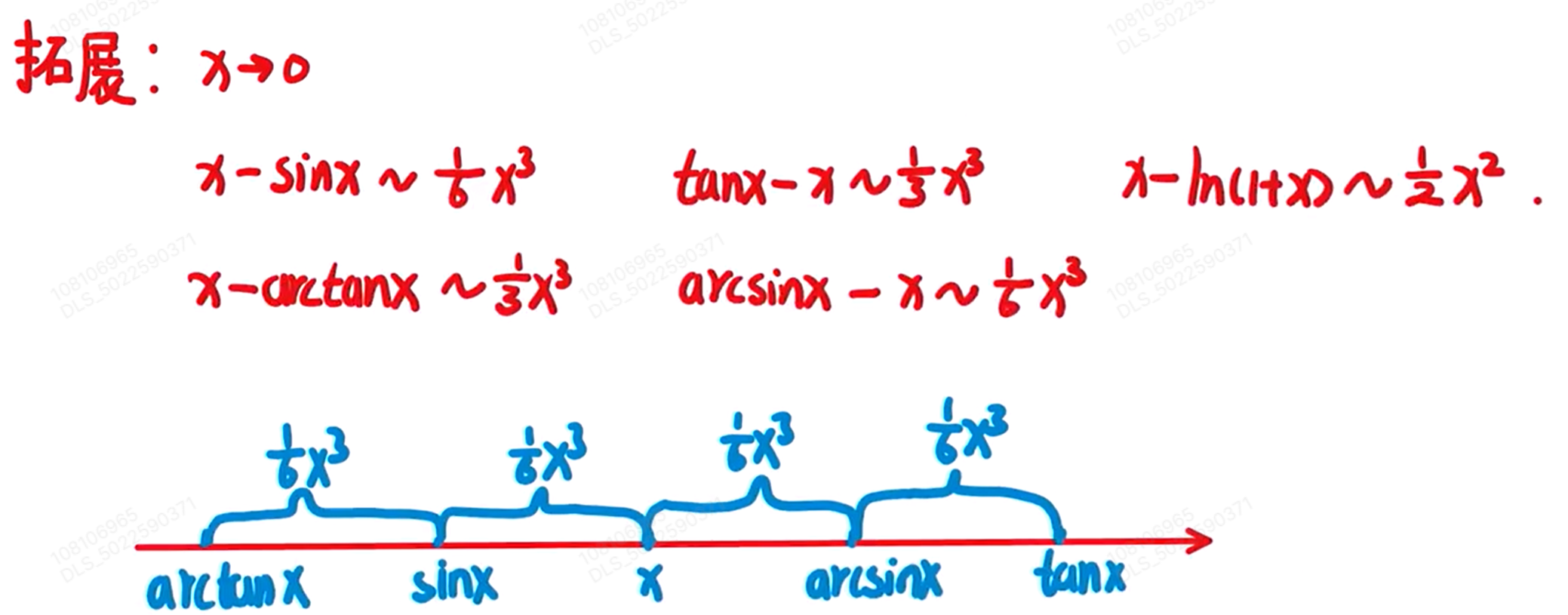
2. 泰勒展开

2.1. 几个常用的展开式

函数	展开式
$e^x$	$1+x+\frac{x^2}{2!}+\frac{x^3}{3!}+\cdots +\frac{x^n}{n!}$+o($x^n$)
$\sin x$	$x - \frac{x^3}{3!} + \frac{x^5}{5!} - \cdots + (-1)^n \frac{x^{2n+1}}{(2n+1)!}+o(x^{2n+1}) $
$\cos x$	$1-\frac{x^2}{2!}+\frac{x^4}{4!}-\cdots +(-1{)}^n\frac{x^{2n}}{(2n)!}+o(x^{2n})$
$\ln (1+x)$	$x-\frac{x^2}{2}+\frac{x^3}{3}-\cdots +(-1{)}^{n-1}\frac{x^n}{n}+o(x^n)$
$(1+x{)}^a$	$1+ax+\frac{a(a-1)}{2}{x}^2+\cdots +\frac{a(a-1)\cdots (a-n+1)}{n!}{x}^n+o(x^n)$

3. 函数极限

3.1. 七种未定式

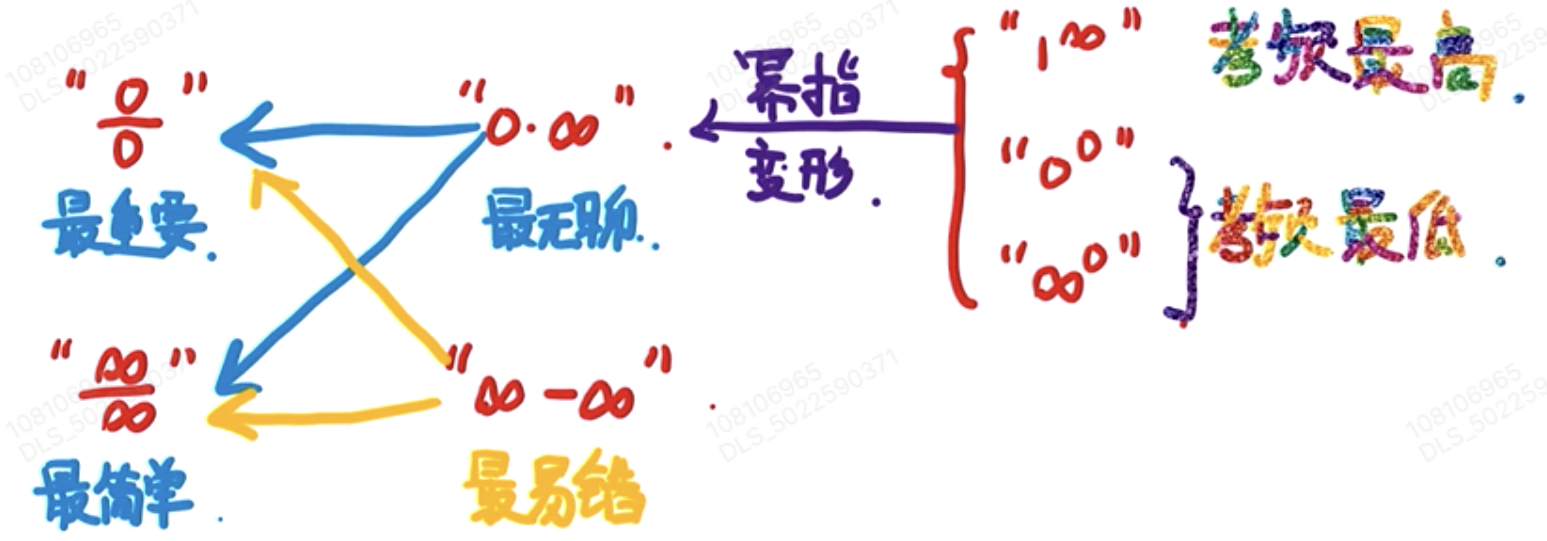
3.2. $0/0$ 型极限

• 泰勒展开；
• 洛必达；
• （二次根号）根式有理化；
• 三次根号
  • 提取因式构造 $(1+ax{)}^{1/3}$
  • （了解）立方差公式有理化：$a^3-b^3=(a-b)(a^2+ab+b^2)$

3.3. $\mathrm{\infty }/\mathrm{\infty }$ 型极限

• $x\to -\mathrm{\infty }$ 时，$x$ 拿进根号里要加 $-1$；
• $\mathrm{\infty }/(\mathrm{\infty }\times 0)$ 型，但是分母无穷阶数高于分子时，把分母的无穷部分提到分子，变成 $0/0$ 型；

4. n 项和数列极限

4.1. 0-1 定积分

• 定义

  $${\int }_0^{1}f(x)\mathrm{d}x=\underset{n\to \mathrm{\infty }}{lim}\frac{1}{n}\sum _{i=1}^{n}f(x_i)$$

• $x_i$ 表示在 $n$ 个小区间 $[0,\frac{1}{n}),[\frac{1}{n},\frac{2}{n}),\cdots ,[\frac{n-1}{n},1)$ 中每个区间任取一点。常见的有取两个端点或取中点，即

  $$x_i=\frac{i}{n},\frac{i-1}{n},\frac{2i-1}{2n}$$

• 拓展 1：可以添加/缺少有限项 $f(x_j)$，例如

  $$\underset{n\to \mathrm{\infty }}{lim}\frac{1}{n}(\frac{1}{1+(\frac{2}{n}{)}^2}+\frac{1}{1+(\frac{3}{n}{)}^2}+\cdots +\frac{1}{1+(\frac{n+1}{n}{)}^2})$$

• 拓展 2：总系数 $\frac{1}{n}$ 不固定，在 $n\to \mathrm{\infty }$ 时与 $\frac{1}{n}$ 等价/同阶的无穷小都可以作为总系数，例如 $\frac{1}{n+1}$。

• 拓展 3：对于任意区间 $[a,b]$ 定积分，换元，转换到 0-1 区间定积分。

4.2. 夹逼

• 将分母/分子分别往大/小放缩，得到两个新数列。新数列要有相同极限 $a$。
• 注意：由夹逼准则定义，不一定要全部放缩，从某项开始放缩也可以。
• 常用分式放缩：放缩分母，分别将分母放缩为求和式中最大和最小的分母，通分化简。
• 可能需要和定积分法结合，先放缩再定积分法求极限。

5. 无穷小比较

5.1. 变限积分无穷小比较

• 二级结论：$x\to 0$ 时可直接对变限积分的被积函数进行无穷小等价，即

  $${\int }_0^{\varphi (x)}f(t)\mathrm{d}t\sim {\int }_0^{\varphi (x)}g(t)\mathrm{d}t(x\to 0)$$

  需要满足三个条件：

  • $f(x),g(x)$ 在 $x=0$ 去心邻域可导。
  • $x\to 0$ 时，$f(x)/g(x)\to 1$，不要求 $f(x),g(x)$ 是无穷小。
  • $\underset{x\to 0}{lim}\varphi (x)=0$，$\varphi (x)$ 在 $x=0$ 去心邻域可导且 ${\varphi }^{\prime }(x)\ne 0$。

• 注意：积分上限函数不同时，即使被积函数等价了也不能直接相比，必须算出积分再比！

6. 函数的间断点

6.1. 间断点枚举

• 分母为 0 的点（总分母，各种指数上的小分母都要考虑）。
• 函数无定义点（一般 $\ln x$，$\tan x$）.

6.2. 带极限函数

• 极限变量一般不是 $x$ 而是其指数 $n$。
• 要先解出极限，求出 $f(x)$，再求间断点。$f(x)$ 一般是分段函数。

7. 渐近线

7.1. 水平/竖直渐近线

• 竖直渐近线：定义域端点、无定义点、分段点处，若极限为 $\mathrm{\infty }$，则 $x=x_0$ 为竖直渐近线。
  • 两侧极限不一定要相同，都趋于 $\mathrm{\infty }$ 就可以。
• 水平渐近线：$x\to \mathrm{\infty }$ 时的极限 $y=A$。

7.2. 斜渐近线 ($k\ne 0$)

• 同一趋近条件下，如果已经有水平渐近线，则其就是 $k=0$ 的线，不用再求斜渐近线。
  • 不同趋近条件下（如 $x\to +\mathrm{\infty },x\to -\mathrm{\infty }$）要分开考虑。
• 斜渐近线 $y=kx+b$，先求 $k$ 再求 $b$
  • $k=\underset{x\to \mathrm{\infty }}{lim}f(x)/x$，若存在再求 $b$，若不存在则斜渐近线不存在。
  • $b=limx\to \mathrm{\infty }(f(x)-kx)$，若存在，则斜渐近线 $y=kx+b$。

8. 数列极限存在性

8.1. 单调有界 v.s. 收敛

单调有界强于收敛，收敛不能推得单调有界。反例

$$x_n=(-1{)}^n\frac{1}{n}$$

8.2. 复合函数数列收敛性

函数数列 $f(x_n)$ 内层 $x_n$ 收敛，外层 $f(x)$ 单调有界，不能推得 $f(x_n)$ 收敛。反例

$$\begin{array}{rl}f(x)& =\{\begin{array}{ll}\arctan x+1& x\ge 0\\ \arctan x-1& x<0\end{array}\\ x_n& =(-1{)}^n\frac{1}{n}\end{array}$$

即可以构造分段函数使得 $f(x_n)$ 的不同子序列有不同极限，从而整体数列极限不存在。