题目
不定积分
1.
分子分母都是
的形式,前面直接为整数,后面积分成
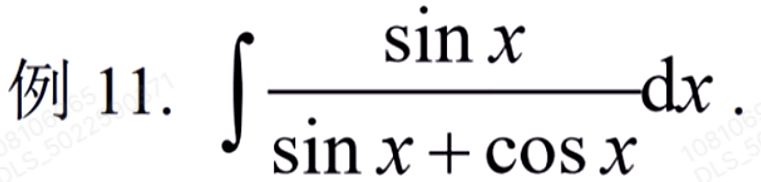
不定积分
1.
第二问,双常数(积分上下限都是常数),一般令上限为自变量
注意左边积分上限中的

2.
奇偶性排除掉分子的
法一:看到
统一三角函数形式,
用华理士公式计算。
法二:分式有理化。
第一项常数积分,第二项数形结合面积法。
3.
被积函数周期为
注意
4.
- 分母为
且分子较为简单时,应优先考虑凑微分 。 - 倍角公式,
然后分部积分。
分子分母都是
的形式,前面直接为整数,后面积分成
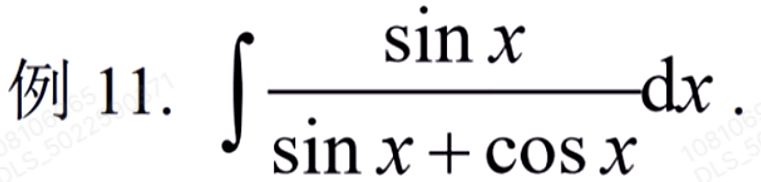
第二问,双常数(积分上下限都是常数),一般令上限为自变量
注意左边积分上限中的

奇偶性排除掉分子的
法一:看到
统一三角函数形式,
用华理士公式计算。
法二:分式有理化。
第一项常数积分,第二项数形结合面积法。
被积函数周期为
注意
然后分部积分。