（二）浮点数

1. 浮点数

1.1. 浮点数格式

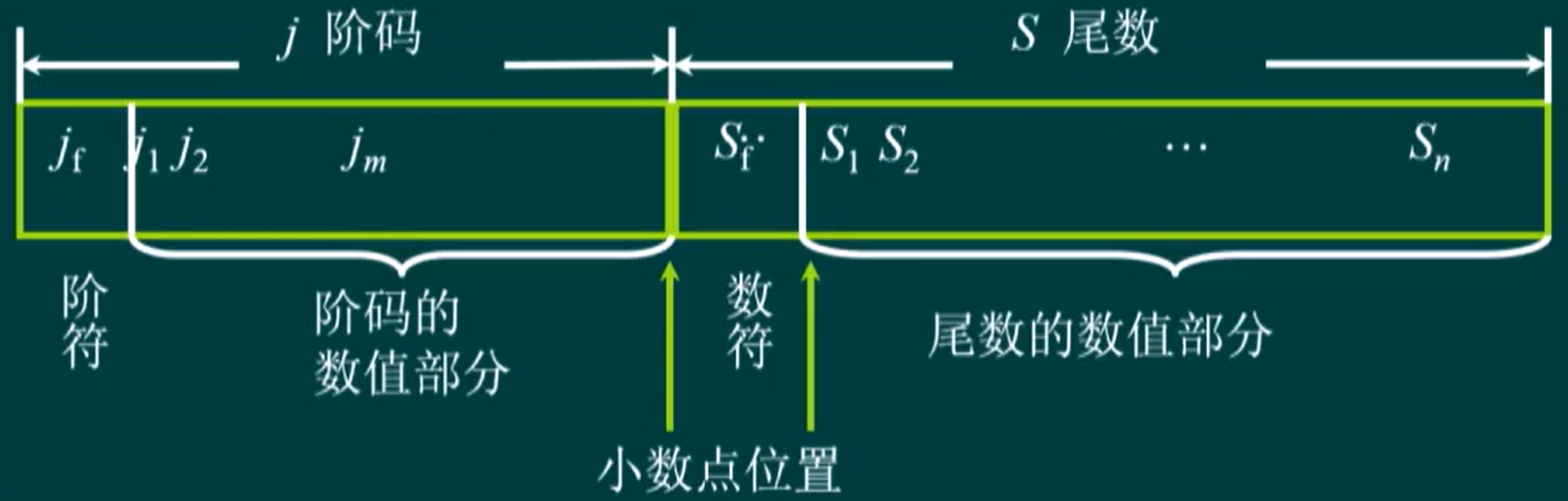
• 浮点数 N：$N=S\times r^j$;

  • $S$：尾数，为一个带符号定点小数；

  • $r$：基数，取 2 的次方，如 2，4，8，16 等**（一般取 2）**；

  • $j$：阶码，为一个带符号定点整数；

• 尾数决定浮点数精度，即能表示小数点后的位数；

• 阶码：决定浮点数能表示的范围；

• 实例分析：浮点数长 16 位，$r=2$，阶码 5 位含符号位 1 位，尾数 11 位含符号位 1 位，都用原码形式，写出 $-53/512$ 的浮点形式；

  • 1）写成科学计数法：$-53/512=(-53)\times 2^{-9}$；

  • 2）分析尾数取值：规格化

    • 负数，符号位为 1；

    • 因为 $(53{)}_{10}=(110101{)}_2$，$\times 2^{-9}$ 需要将小数点左移 9 位，而原数规格化只能移 6 位，所以还有 3 位要放到阶码上；

      • 规格化：指尾数数据位的最高位必须是有效值（原码为 1，补码和反码为 0）；

    • 所以尾数取值为 $S=(1.1101010000{)}_2$，注意右侧补 0；

  • 3）分析阶码取值：由于还剩 3 位没移，因此阶码 $j=-3$，负数符号位为 1，原码表示为 $j=(10011{)}_2$；

  • 因此，浮点数表示为（先阶码后尾数）：$(1001111101010000{)}_2$；

• 可以看出，要点在于确定尾数取值，尾数规格化自带移位，剩下的移位用阶码完成；

• 规格化尾数的浮点数精度是最高的；

1.2. 浮点数的范围

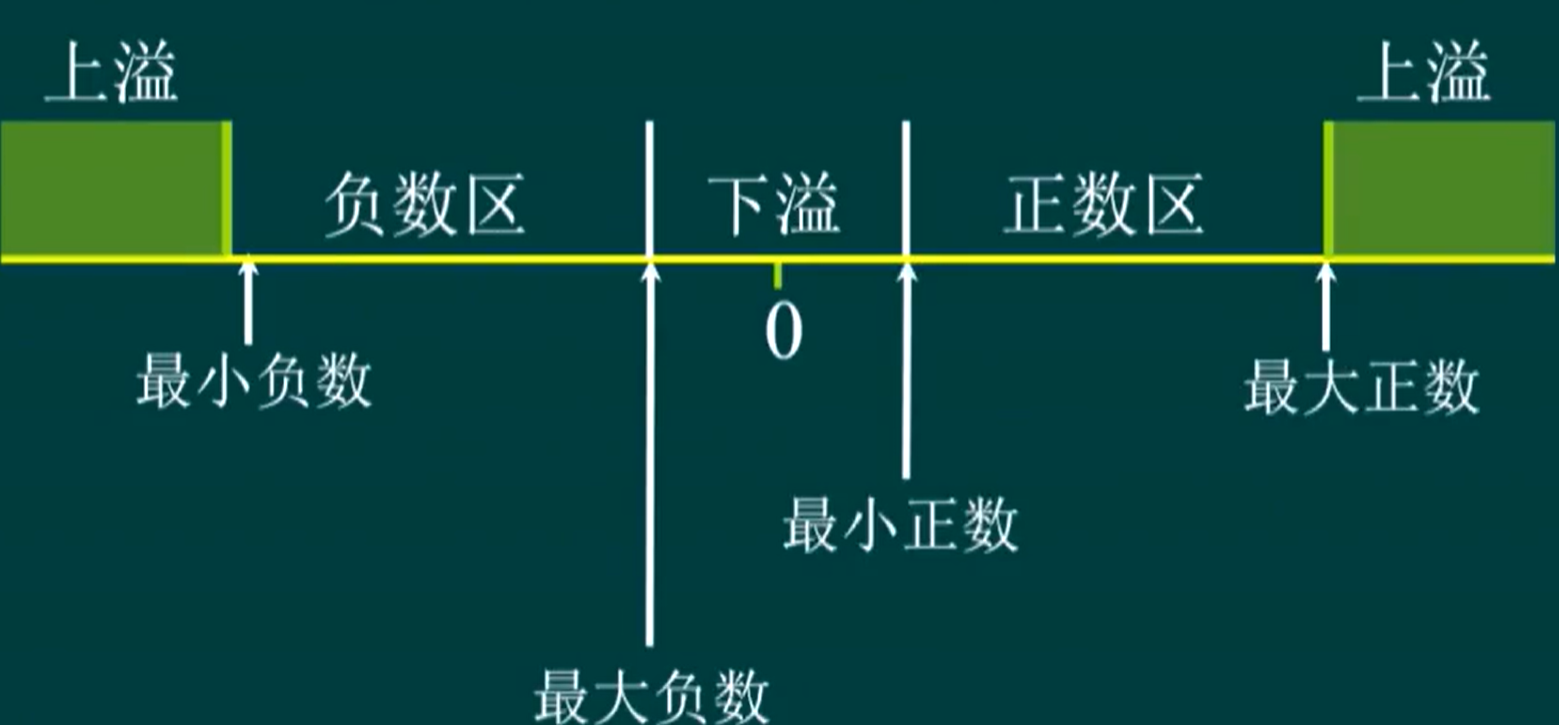
• 由 $N=S\times r^j$，先算出 $S$ 和 $j$ 的范围，再计算即可；

• 注意

  • 考虑规格化与否，会导致尾数表示范围不同；

    • 规格化要求尾数最高位必须为 1；

  • $S$ 和 $j$ 采用不同码表示时，范围不同，对应 $N$ 的范围也会不同；

  • $r^j$ 始终为正，$N$ 正负由 $S$ 决定；

• 下溢：0 和最大负数，0 和最大正数之间的数无法用浮点数表示（注意 0 可以）；

  • 处在下溢区间的数被当作机器 0，不会报错；

  • 与之对比，上溢会产生 overflow 错误；

1.3. 补码规格化

• 左规：补码运算结果未溢出，但不是规格化，需要将尾数数据位左移，直到满足规格化；

  • 尾数左移 1 次，阶码需要减 1；

• 右规：补码运算结果溢出，将尾数数据位右移 1 次；

  • 采用两位符号位时，符号位低位移到数据位最高位，符号位补成相同两位；

  • 阶码对应地加 1；

• 实例分析：采用两位符号位，00 表示正，11 表示负；

  • 左规：$(00.0...{)}_2$ 或 $(11.1...)$，需要数据位左移直到最高位为有效位；

  • 右规：$(10....)$ 或 $(01....)$，数据位右移 1 位；

    • 右移后，$(10....)\to (11.0...)$，$(01....)\to (00.1...)$；

1.4. 机器 0

• 尾数 $S=0$ 时，无论阶码 $j$ 为何值，都按机器 0 处理；

• 阶码 $j\le j_{\min }$，即 $j$ 小于等于其能表示的最小值时，无论尾数 $S$ 为何值，都按机器 0 处理；

⭐2. IEEE 754 标准

2.1. 格式

• 短实数：总 32 位，符号位 1 位，阶码 8 位，尾数 23 位；

• 长实数：总 64 位，符号位 1 位，阶码 11 位，尾数 52 位；

• 临时实数：总 80 位，符号位 1 位，阶码 15 位，尾数 64 位；

2.2. 表示方式

• 尾数：原码规格化形式，最高位固定为有效值 1；

  • 最高位固定为 1，所以通常省略不写，因此，$n$ 位尾数可表示 $n+1$ 位定点小数；

• 阶码：偏移形式，即阶码真值加上一个偏移 $j=j_{\mathrm{real}}+\mathrm{offset}$；

  • 短实数：偏移 $127=(7F{)}_{16}$；

  • 长实数：偏移 $1023=(3FF{)}_{16}$；

  • 临时实数：偏移 $16383=(3FFF{)}_{16}$；

• 实例分析

  • 1. 将十进制数 178.125 表示为 IEEE 754 标准浮点数（32 位短实数）；

    • 1）表示为二进制真值，即 $(178.125{)}_{10}=(10110010.001{)}_2$；

    • 2）小数点移到最左边，表示为 $S\times 2^j$，即 $(10110010.001{)}_2=(1.0110010001{)}_2\times 2^7$；

    • 3）阶码 $j=7+127=134=(10000110{)}_2$；

    • 4）尾数首位 1 省略，后面要补零，凑到 23 位 $S=(01100100010...{)}_2$；

    • 5）组装：$F=(0100001100110010001000...{)}_2$；

    • 6）一般是写为 16 进制，$F=(4332200{)}_{16}$；

  • 2. IEEE 754 标准浮点数 $F=(C6400000{)}_{16}$，求其十进制值；

    • 1）写为二进制：$F=(110001100100000000...{)}_2$；

    • 2）符号位 $\mathrm{sym}=1$，阶码 $j=(10001100{)}_2$，尾数**（还原最高位 1）** $S=(1.100000000..{)}_2$；

    • 3）阶码真值 $j_{\mathrm{real}}=j-\mathrm{offset}=140-127=13$，尾数 $S=1.5$，所以真值为 $F=-1.5\times 2^{13}$；

  • 注意事项：1）最高一位是符号位，2）尾数最高位 1，转为二进制要省略，转回十进制要还原；

2.3. 范围（以 32 位短实数为例）

• 阶码特殊值

  • 阶码全 1：表示无穷大；

  • 阶码全 0：表示机器 0；

• 尾数范围（不考虑符号）：$S_{\min }=(1.000...{)}_2=1$，$S_{\max }=(1.1111...{)}_2=2-2^{-23}$，注意后面是 23 个 1；

• 阶码范围：$j_{\min }=(00000001{)}_2-127=-126$，$j_{\max }=(11111110{)}_2-127=127$；

• 绝对值范围：$|F{|}_{\min }=2^{-126}$，$|F{|}_{\max }=(2-2^{-23})\times 2^{127}$；

• 表示范围：正负数的表示范围是对称的，即 $[-|F{|}_{\max },-|F{|}_{\min }]\cup [|F{|}_{\min },|F{|}_{\max }]$；

3. 浮点数加减法

3.1. 对阶

• 含义：两个浮点数 $F_1=S_1\times 2^{j_1}$ 和 $F_2=S_2\times 2^{j_2}$ 加减时，需要将阶码变换到相等，才能运算；

• 方法：小阶向大阶对齐，小阶的尾数右移；

  • 不能大阶对小阶的原因：大阶变小会使得尾数左移，可能超过 1，造成溢出；

  • 计算阶差 $\mathrm{\Delta }j=|j_1-j_2|$，然后小阶码变为大阶码，小阶码的尾数向右移动 $\mathrm{\Delta }j$ 位；

    • 尾数为原码，则符号位不参与移位，高位补 0；

    • 尾数为补码，符号位一起移位，高位补符号位；

3.2. 规格化

• 对阶完成的浮点数 $F_1$ 和 $F_2$，可以直接对尾数进行加减运算；

• 然后需要对尾数进行规格化操作；

• 可能发生左规和右规的情况；

3.3. 舍入

• 在对阶和右规操作中，尾数的低位可能被移掉；

• 0 舍 1 入法：若移掉的是 0 则直接舍弃，若是 1 则要进位；

• 去尾法：直接舍弃；

3.4. 判断溢出

• 浮点数判断溢出较为复杂：

  • 根据定义：超过浮点数能表示的范围，才叫溢出；

  • 尾数溢出，浮点数不一定溢出；

  • 阶码溢出：浮点数一定溢出；

  • 注意机器 0 的情况；

• 运算结束后，对阶码进行判断：上溢 or 下溢；

• 阶码上溢：需要置位溢出表示；

• 阶码下溢：结果置为机器 0；

• 实例分析：令 $X=2^{(010{)}_2}\times (0.11011011{)}_2$，$Y=2^{(100{)}_2}\times (-0.10101100{)}_2$。浮点数阶码 6 位，尾数 10 位，均为补码形式，符号位 1 位。求 $X+Y$；

  • 1）写出二者尾数补码形式 $S_X=(0.110110110{)}_2$，$S_Y=(1.010101000{)}_2$；

  • 2）$j_X=2$，$j_Y=4$，所以 $X$ 需要变换，阶码变为 4，尾数右移 2 位；

  • 3）注意到 $S_X$ 倒数第二位为 1，右移时需要舍入进位，即最低位 + 1。右移两位后，$S_X^{\prime }=(0.001101110{)}_2$；

  • 4）对阶完成，二者尾数相加：$S_X^{\prime }+S_Y=(1.100010110{)}_2$，阶码为 $j_Y=4=(000100{)}_2$；

习题

• 1. 16 位浮点数，阶符 1 位，阶码 6 位，数符 1 位，尾数 8 位，当采用补码表示时，所能表示的数的范围是（）

  • A. $[-2^{64},2^{64}\times (1-2^{-8})]$

  • B. $[-2^{63},2^{63}\times (1-2^{-8})]$

  • C. $[-2^{63},2^{63}\times (1-2^{-9})]$

  • D. $[-2^{63}\times (1-2^{-8}),2^{63}\times (1-2^{-8})]$

  • 答案：B

  • 解析：阶码 7 位带符号定点整数，尾数 9 位带符号定点小数，$N=S\times 2^j$；

    • 最大值：$S$ 和 $j$ 同时取最大正数，$S_{\max }=1-2^{-8}$，$j_{\max }=2^6-1=63$，所以 $N_{\max }=2^{63}\times (1-2^{-8})$；

    • 最小值：$S$ 取最小负数，$j$ 最大正数，$S_{\min }=-1$，所以 $N_{\min }=-2^{63}$；

• 2. 机器字长 32 位，浮点数阶码 8 位，尾数 24 位，各含 1 位符号。求：最小的规格化正数是多少？

  • 答案：$2^{-129}$；

  • 解析：

    • 阶码最小 $j_{\min }=-2^7=-128$；

    • 尾数规格化要求最高位为 1，令其余都为 0，则 $S_{+\min }=(0.100...{)}_2=2^{-1}$；

    • 所以 $N_{+\min }=2^{j_{\min }}\times S_{+\min }=2^{-129}$；

• 3. 两个 32 位 IEEE 754 浮点数，$F_1=(CC900000{)}_{16}$，$F_2=(B0C00000{)}_{16}$，则

  • A. $F_1<F_2$ 且同号；

  • B. $F_1<F_2$ 且异号；

  • C. $F_1>F_2$ 且同号；

  • D. $F_1>F_2$ 且异号；

  • 答案：A

  • 解析

    • 快速比较浮点数大小：尾数决定精度，阶码决定范围（大小）

    • 因为 $F_1$ 和 $F_2$ 二进制首位都是 1，所以都是负数，同号；

    • 观察到 $F_1$ 二进制的第二位为 1，而 $F_2$ 二进制第二位为 0，则阶码必有 $S_1>S_2$；

      • 且差距极大（至少差 $2^7=128$），可以忽略尾数的作用；

    • 则绝对值有 $|F_1|>|F_2|$，由于是负数，所以 $F_1<F_2$；

• 4. 浮点数阶码和尾数均补码形式，阶码 5 位，尾数 7 位，均含两位符号位。令 $X=29/32\times 2^7$，$Y=5/8\times 2^5$，则 $X+Y$ 为

  • A. $(001111100010{)}_2$；

  • B. $(001110100010{)}_2$；

  • C. $(010000010001{)}_2$；

  • D. 溢出；

  • 答案：D

  • 解析：

    • $S_X=(00.11101{)}_2$，$j_X=7$，$Y=(00.10100{)}_2$，$j_Y=5$；

    • 先对阶，$S_Y^{\prime }=(00.00101{)}_2$，$j=j_X=7=(00111{)}_2$；

    • 然后相加，$S=S_X+S_Y^{\prime }=(01.00010{)}_2$，发生溢出，需要右规；

    • $S^{\prime }=(00.10001{)}_2$，对应阶码需要加 1，即 $j^{\prime }=j+1=8=(01000{)}_2$，阶码发生溢出，故结果溢出；

• 5. 下列叙述中，正确的有（）

  • (1). 对阶操作不会引起阶码上溢或下溢，(2). 右规和尾数舍入都可能引|起阶码上溢，(3). 左规时可能引起阶码下溢，(4). 尾数溢出时结果不一定溢出；

  • A. (2), (3)；

  • B. (1), (2), (4)；

  • C. (1), (3), (4)；

  • D. 全部；

  • 答案：D

  • 解析

    • (1)：对阶是把小阶变大阶，不会溢出，对；

    • (2)：右规，阶码需要 + 1，可能溢出。舍入，尾数低位 +1，可能导致尾数溢出，进而右规，进而导致阶码溢出，对；

    • (3)：左规：阶码需要 -1，可能会下溢，对；

    • (4)：正确；

• 6. 有下列 C 语言写成的函数 f1，其中 unsigned 和 int 类型都是 32 位，float 是 IEEE 754 单精度标准；

  int f1(unsigned n) {
      int sum = 1, power = 1;
      for (unsigned i = 0; i <= n - 1; ++i) {
          power *= 2;
          sum += power;
      }
      return sum;
  }

  • 6.1. n=0 时，会出现死循环，为什么？若将变量 i 和 n 都改为 int，是否还会死循环？为什么？

  • 6.2. 将 f1 中的 int 都改为 float 得到 f2，f1(23) 和 f2(23) 的返回值是否相等？机器数（16 进制）各是多少？

  • 6.3. f1(24)=33 554 431，f2(24)=33 554 432.0，二者为什么不相等？

  • 6.4. f1(31)=-1，而不是 2^32-1，为什么？若要使得返回值与期望的值相等，n 最大为多少？

  • 6.5. f2(127)=0x7F80 0000，对应的值是什么？若要使 f2(n) 不溢出，最大的 n 是多少？若要 f2(n) 结果精确无舍入，n 最大多少？

  • 解析

  • 6.1

    • $n=0$ 时，因为 $n$ 无符号，所以有 $(u32{)}_{\min }-1=(u32{)}_{\max }$，故 $i\le n-1$ 恒成立，会出现死循环；

    • $n=0$ 但 $n$ 有符号时，$n-1$ 为负数，$i\le n-1$ 不成立，不会进入循环，所以不会死循环；

  • 6.2

    • 由代码知，$f_1(n)=1+\sum _{i=0}^{n-1}{2}^{i+1}=2^{n+1}-1$，故 $f_1(23)=2^{24}-1$；

    • 整数形式下，$2^{24}-1=(00FFFFFF{)}_{16}$；

    • IEEE 754 形式下，小数点移到第一个 1 后面，为 $(1.11111111111111111111111{)}_2\times 2^{23}$；

      • 则 $S=(7FFFFF{)}_{16}$，$j=23+127=150=(10010110{)}_2$；

      • 则 $F=(010010110S)=(4B7FFFFF{)}_{16}$；

  • 6.3. 原因是尾数右规产生了舍入误差

    • $f_1(24)=f_2(24)=2^{25}-1$，没有超出 int 范围，故 int 能正常表示；

    • 对于 IEEE 754，小数点移到第一个 1 后，为 $(1.111111111111111111111111{)}_2\times 2^{24}$；

    • 此时，省略高位的 1 也要 24 位才能表示尾数，故溢出，需要舍入，由 0 舍 1 入知最低为 +1；

    • 舍入进位后，尾数为 $(10.0000000...{)}_2$，需要右规，阶码对应 + 1，变为 25；

    • 最后，$F$ 的尾数全 0，阶码真值为 25，因此 $F=S\times 2^j=2^{25}=33554432.0$，产生了舍入误差；

  • 6.4

    • $f_1(31)=2^{32}-1$ 超出了 int 表示范围。若表示为 u32 则为全 1，全 1 在有符号 int 补码下为 -1；

    • $n$ 最大为 30，此时 $f_1(30)=2^{31}-1$，恰为 i32 最大正数；

  • 6.5.

    • 法一：展开 $(7F800000{)}_{16}$，发现阶码部分为全 1，故发生上溢，为无穷大；

    • 法二：32 位 IEEE 754 浮点数表示的最大正数是 $M=(2-2^{-23})\times 2^{127}=2^{128}-2^{104}$，而 $f_2(127)=2^{128}-1>M$，故上溢；

    • 因为 $2^{127}-1<M<2^{128}-1$，故 $n$ 最大值可取 126；

    • 由 6.3 知，尾数位数不能超过 23，即结果的位数不能超过 24，即 $f(23)=2^{24}-1$，因此 $n$ 最大值为 23；

  • 结论

    • 若用定点数和浮点数的计算结果相差 1，一般是尾数舍入误差；

    • 若二者误差很大，一般是溢出；

• 粗体代码：boldcode