（一）进制系统和定点数

1. 进制系统

1.1. 除基取余法（整数十转二进制）

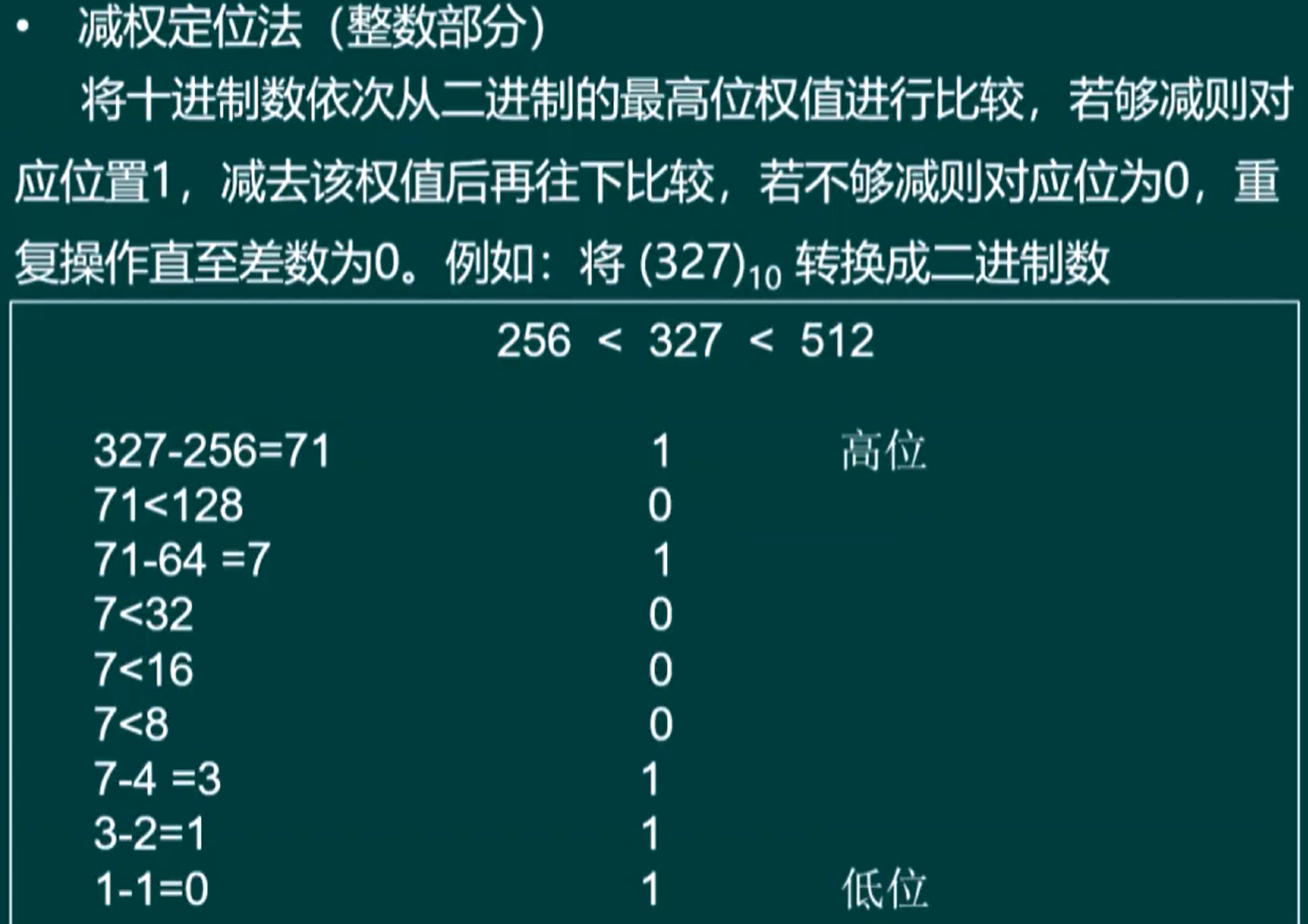
1.2. 减权定位法（整数十转二进制）

1.3. 乘基取整法（小数十转二进制）

1.4. 十进制转十六进制 / 八进制

• 例：327.8125 转 16 进制 $(327.8125{)}_{10}=(101000111.1101{)}_2=(147.D{)}_{16}$；

• 反之亦然：先化为二进制，再转十进制；

2. 定点数

2.1. 真值和机器数

• 真值：二进制绝对值及其正负的直接表示（带符号绝对值）；

  • 如：$X=+1101$，$Y=-1011$；

• 机器数：符号位用二进制表示，一般 0 表示正，1 表示负；

  • 如：$X=11101$，$Y=01011$

2.2. 定点数

• 概念：定点整数/小数，原码，补码，反码，移码；

• 有符号/无符号数

  • 无符号数：每一位都用来表示数值，恒正；

    • $n$ 位无符号数的范围：$0\sim 2^n-1$；

  • 有符号数：用一位 (一般最高位) 来表示符号，其余表示数值。如：原码，补码，反码，移码；

• 原码：最高位符号位，其余按原样表示数值，等价于机器数；

• 补码：最高位符号位，其余表示数值。正数数值为其自身，负数数值为 (模数 - 绝对值) ；

  • 补数：一个正数和负数绝对值之和为模数 M，则称这两个数在模 M 意义下互为补数（模 M 同余）；

  • 模数：对于固定的 n 位二进制，其模数为 $M=2^n$，即一个最高位为 1 其余全 0 的 n+1 位二进制；

  • 因此，数值部分正数 $(x{)}_{\mathrm{补}}=x$，负数 $(x{)}_{\mathrm{补}}=M-|x|$；

• 反码：基本和补码相同，负数的数值部分还要减去 1；

• 移码：方便比较真值大小。只能表示整数；

  • n 位二进制的移码 $(x{)}_{\mathrm{移}}=2^n+x$；

  • 可以推知：若 $x$ 为负数（有效范围内），则 $x$ 的补码和移码除最高位外相同；

2.3. 真值和机器数的化简方法

• 1）最高位符号位，一般用逗号和其他位隔开；

• 2）正数：符号位 0，原码 = 补码 = 反码；

• 3）负数：符号位 1，数值部分首先求原码（绝对值）

  • 反码：数值部分按位取反；

  • 补码：数值部分按位取反再 +1；

  • 移码：先算补码，符号位置为 0 即可；

• 注意：定点小数的补码可表示 -1，但其原码并不能表示 1，因此约定 $(1.000...0{)}_{\mathrm{补}}=-1.0$；

2.4. ±0 的表示

• 原码：±0 的表示法不同（符号位不同）；

• 补码：±0 的表示法相同（都是全 0）；

• 反码：±0 的表示法不同（一个全 0 一个 全 1）；

• 移码：±0 的表示法相同；

3. 数据转换

3.1. 短转长

• 位数较短的数转换为较长的数；

• 方法：用符号位填充（正数填 0，负数填 1）

• 例：32 位 int 转换为 64 位 long；

• 自动类型转换；

3.2. 长转短

• 位数长的数转换为较短的数；

• 方法：截取低位；

• 例：16 位 short 转 8 位 char；

• 强制类型转换，一般慎用，容易出问题；

3.3. 整数和浮点互转

• 整数转浮点：小数位全部为 0；

• 浮点转整数：去掉小数尾；

3.4. 有符号数和无符号数互转

• 有符号数转无符号数：符号位也当作数据位；

• 无符号数转有符号数：最高位直接当作符号位；

4. 定点数运算

4.1. 移位运算

• 逻辑移位

  • 适用：无符号数；

  • 左移：高位丢弃，低位补 0，相当于乘 2；

  • 右移：低位丢弃，高位补 0，相当于整除 2；

• 算术移位

  

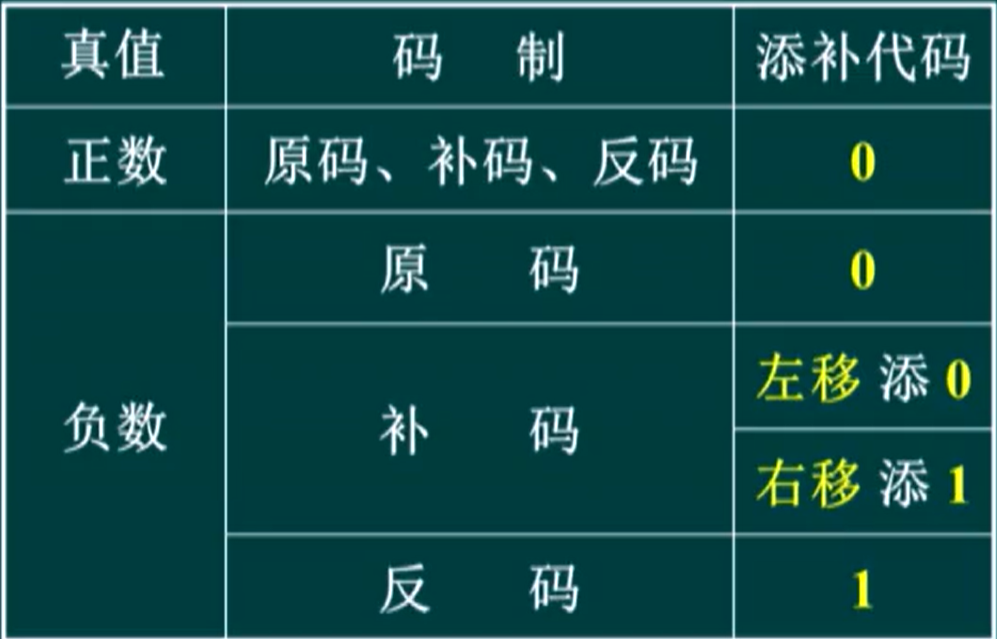
  • 适用：有符号数；

  • 符号位不变；

  • 补码补位规则的解析

    • 补码可看作 (反码 | 原码) 的组成，即以某一位分界，其高位为反码形式，其低位为原码形式；

    • 判断：从低往高位的第一个 1 为界，它及其低位部分为原码，其高位部分为反码形式；

      • 原码和补码相互转换可用此方式快速计算；

      • 原转补和补转原都是一样判断；

    • 反码移位补 1，原码移位补 0，因此左移 0 右移 1；

  • 算术左移：相当于乘 2；

  • 算术右移：相当于整除 2（floor）；

    • 例：-13 右移一位为 -7；

4.2. 加减运算

• 一般是指补码之间的运算；

• 对于原码、反码：数据位加减，符号位不参与运算；

• 定点小数和定点整数的计算方式相同；

• 加法运算

  • $(x{)}_{\mathrm{补}}+(y{)}_{\mathrm{补}}=(x+y{)}_{\mathrm{补}}$：直接将补码二进制连符号位相加即可；

• 减法运算

  • $(x{)}_{\mathrm{补}}+(y{)}_{\mathrm{补}}=(x{)}_{\mathrm{补}}+(-y{)}_{\mathrm{补}}$：转化为加法；

  • 快速将 $(y{)}_{\mathrm{补}}$ 互转 $(-y{)}_{\mathrm{补}}$：连同符号位一起按位取反，再低位 +1；

4.3. 机器数表示范围

• 原码、反码：按照定义找最大和最小值即可（一般是填全 0/全 1）；

• 补码

  • 最大正数：数据位全填 1；

  • 最大负数：数据位最低位填 1 其他全 0（取反 +1 要求至少有一个 1）；

• 设机器数 $n$ 位，其中一位符号位，则

  • 原码

    • 定点整数：最大 $2^{n-1}-1$，最小 $-(2^{n-1}-1)$；

    • 定点小数：最大 $1-2^{-(n-1)}$，最小 $-(1-2^{-(n-1)})$；

  • 反码：一样的；

  • 补码

    • 定点整数：最大 $2^{n-1}-1$，最小 $-2^{n-1}$；

    • 定点小数：最大 $1-2^{-(n-1)}$，最小 $-1$；

4.4. 溢出判断

• 溢出：要表示的数超过了定点数能表示的范围；

• 一般是指补码运算时发生溢出；

• 判断运算结果发生溢出：运算结果符号和预期符号相反；

  • 如：正 + 正 = 负，正 - 负 = 负，负 + 负 = 正，负 - 正 = 正；

• 计算机判断：若符号位的进位 xor 最高数据位的进位 = 1，则发生溢出；

  • 符号位进位：直接用两个数符号位相加，判断进位；

  • 最高数据位进位：直接用两个数最高数据位相加，判断进位；

  • 无法判断是正溢出 or 负溢出；

• 改进的计算机判断：采用两位符号位（变形补码）；

  • 用 00 表示正数，11 表示负数；

  • $S=S_1+S_2$，若 $S$ 两符号位相同，则未溢出，否则溢出；

    • 判断法：$V={\mathrm{sym}}_1\mathrm{xor}{\mathrm{sym}}_2$，${\mathrm{sym}}_1$ 为高位，若 $V=1$ 则溢出，否则未溢出；

    • 若溢出且 ${\mathrm{sym}}_1=1$，则发生负溢出（10）；

    • 若溢出且 ${\mathrm{sym}}_1=0$，则发生正溢出（01）；

习题

• 1. 机器字长 8 位，最高位符号位，求下列数字的原码、补码和反码：(1) -35/64，(2) 23/128，(3) -127，(4) -1；

  • 解析：对 $x/2^n$ 型的小数，即在整数 $x$ 二进制的基础上将小数点左移 $n$ 位（类比十进制小数）；

    • 定点小数，小数点默认在最高位后，所表示的数绝对值不超过 1，因此若位数不够，应在最右侧小数部分补 0；

    • $(-35/64{)}_{10}=(1.1000110{)}_{\mathrm{原}}=(1.0111001{)}_{\mathrm{反}}=(1.0111010{)}_{\mathrm{补}}$；

    • $(23/128{)}_{10}=(0.0010111{)}_{\mathrm{原}}$，原 = 反 = 补；

    • $(-127{)}_{10}=(11111111{)}_{\mathrm{原}}=(10000000{)}_{\mathrm{反}}=(10000001{)}_{\mathrm{补}}$；

    • $(-1{)}_{10}=(10000001{)}_{\mathrm{原}}=(11111110{)}_{\mathrm{反}}=(11111111{)}_{\mathrm{补}}$；

• 2. 设 $(x{)}_{\mathrm{补}}=(1x_1{x}_2{x}_3{x}_4{x}_5{)}_2$，若要 $x<-16$，则（）

  • A. $x_1\sim x_5$ 至少有一个 1；

  • B. $x_1=0$，$x_2\sim x_5$ 至少有一个 1

  • C. $x_1=0$，其余任意；

  • D. $x_1=1$，其余任意；

  • 答案：B

  • 解析：

    • $(-16{)}_{\mathrm{补}}=(110000{)}_{\mathrm{补}}=(110000{)}_2$，若 $x<-16$ 即 $|x|>16$，取反 +1 后数据位将小于 $(10000{)}_2$，所以 $x_1=0$；

    • 因为补码数据位是原码按位取反后加 1 得到，故数据位至少有一个 1，所以选 B；

    • 补码比较大小：先看符号位正负，若同号，则直接比较数据位大小，数据位大的值就大；

• 3. 设 $(x{)}_{\mathrm{原}}=(1.x_1{x}_2{x}_3{x}_4{)}_2$，若要 $x>-1/2$，则（）

  • A. $x_1=0$，其余任意；

  • B. $x_1=0$，$x_2\sim x_4$ 至少有一个 1；

  • C. $x_1=1$，其余任意；

  • D. $x_1=1$，$x_2\sim x_4$ 至少有一个 1；

  • 答案：A

• 4. 机器字长 8 位，一个数表示为 1000010，则（）

  • A. 无法确定；

  • B. 是一个补码；

  • C. 值为 130；

  • D. 是一个负数；

  • 答案：A

  • 补充常识

    • C 语言里的二进制为补码表示；

    • 解答题里的计算默认采用补码；

• 5. 机器字长 8 位，$x,y,z$ 为整数，用补码表示。$(x{)}_{\mathrm{补}}=(11110100{)}_2$，$(y{)}_{\mathrm{补}}=(10110000{)}_2$，令 $z=x/2+2\times y$，则

  • A. $(z{)}_{\mathrm{补}}=(11000000{)}_2$；

  • B. $(z{)}_{\mathrm{补}}=(00100100{)}_2$；

  • C. $(z{)}_{\mathrm{补}}=(11011010{)}_2$；

  • D. 溢出；

  • 答案：C

  • 解析：注意补码移位规则：符号位不变，左移补 0 右移补 1；

    • $(x^{\prime }{)}_{\mathrm{补}}=(x/2{)}_{\mathrm{补}}=(11111010{)}_2$，$(y^{\prime }{)}_{\mathrm{补}}=(y\times 2{)}_{\mathrm{补}}=(11100000{)}_2$；

    • $(z{)}_{\mathrm{补}}=(x^{\prime }{)}_{\mathrm{补}}+(y^{\prime }{)}_{\mathrm{补}}=(11011010{)}_2$，进位自动舍弃；