笔记

1. 行列式

1.1. 行列式定义

$$\Vert \begin{array}{cccc}{a}_{11}& a_{12}& \cdots & a_{1n}\\ a_{21}& a_{12}& \cdots & a_{2n}\\ ⋮& ⋮& \ddots & ⋮\\ a_{n1}& a_{n2}& \cdots & a_{nn}\end{array}\Vert =\sum (-1{)}^r{a}_{1p_1}{a}_2{p}_2\cdots a_{n{p}_n}$$

• $p_1,p_2,\cdots ,p_n$：表示从第一行、第二行、到第 $n$ 行选出 $n$ 个不同列的元素进行累乘。即 $p_1\ne p_2\ne \cdots \ne p_n$。由定义知，累加一共有 $n!$ 项。
• $r$ 表示 $p_1,p_2,\cdots ,p_n$ 序列中的逆序对数。例如 $r(3,2,1,4)=3$。
• 适合题型：只求行列式中某项的值，例如若干项含 $x$，求行列式结果中 $x^k$ 的系数。

1.2. 行列式计算

• 利用性质变换：转置、数乘、交换行/列、拆分、倍加。化成三角型。

• 三角型行列式：$\parallel A\parallel =a_{11}{a}_{22}\cdots a_{nn}$。

  $$\Vert \begin{array}{cccc}{a}_{11}& a_{12}& \cdots & a_{1n}\\ & a_{12}& \cdots & a_{2n}\\ & & \ddots & ⋮\\ & & & a_{nn}\end{array}\Vert$$
  • 上三角型、下三角型和对角型都是一样。
  • 若是副对角线（左下到右上），则 $\parallel A\parallel =(-1{)}^{n(n-1)/2}\times \prod (\mathrm{对}\mathrm{角}\mathrm{元}\mathrm{素})$

• 行列式展开定理：先用性质化出更多零项，简化计算。

• 范德蒙行列式

  $$\Vert \begin{array}{cccc}1& 1& \cdots & 1\\ a_1& a_2& \cdots & a_n\\ a_1^2& a_2^2& \cdots & a_n^2\\ ⋮& ⋮& \ddots & ⋮\\ a_1^{n-1}& a_2^{n-1}& \cdots & a_n^{n-1}\end{array}\Vert =\prod _{i<j}(a_j-a_i)$$

• 分块行列式

  $$\begin{array}{rl}\Vert \begin{array}{cc}\mathit{A}& \mathit{O}\\ \mathit{O}& \mathit{B}\end{array}\Vert & =\parallel A\parallel \parallel B\parallel \\ \Vert \begin{array}{cc}\mathit{O}& \mathit{A}\\ \mathit{B}& \mathit{O}\end{array}\Vert & =(-1{)}^{mn}\parallel A\parallel \parallel B\parallel \end{array}$$

  $A,B$ 分别是 $m,n$ 阶方阵。

• 行和或列和相等：都加到第一行/第一列，提公因式变全 1，然后消成三角型。

• 爪形：利用对角线元素消除某行或某列，变为三角型。

• 三对角线：设 $\parallel A\parallel =D_n$，行列式展开，求递推关系。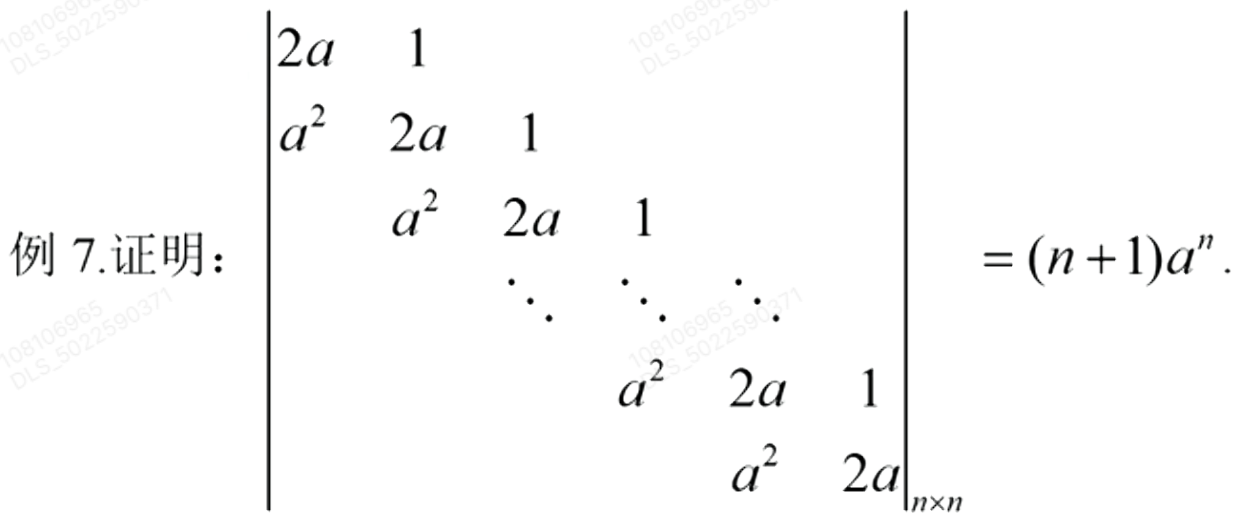

  

  • 按行展开可以得到 $D_n=2a{D}_{n-1}-a^2{D}_{n-2}$，构造等比 $D_n-a{D}_{n-1}=a(D_{n-1}-a{D}_{n-2})$。

  • 如果是证明题，也可以用数学归纳法；计算题则老实算等比求和。

1.3. 抽象行列式计算

• 行列式性质：见 1.2。

• 矩阵的性质：数乘、矩阵乘、逆矩阵、伴随矩阵的行列式。

• 特征值：$\parallel A\parallel ={\lambda }_1{\lambda }_2\cdots {\lambda }_n$

  

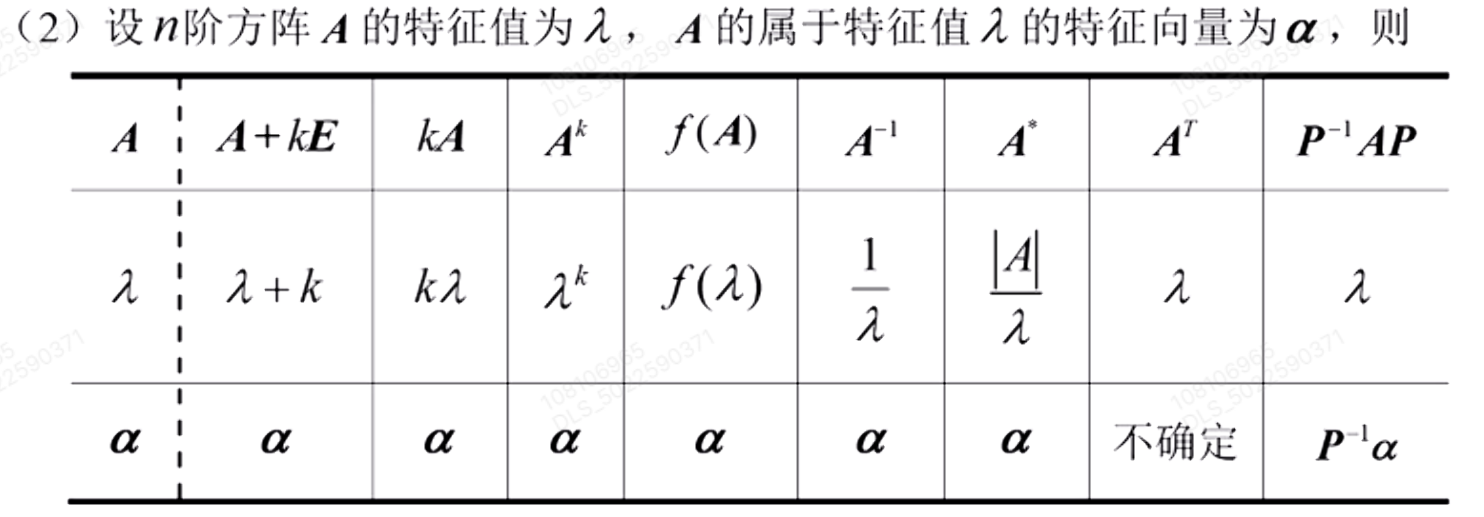
  • 用途：已知 $\parallel A\parallel$，求一个与 $A$ 相关式子的行列式。

• 单位矩阵展开：$E=A^{-1}A=A{A}^{-1}$，展开单位矩阵提公因式，变加为乘。

• 相似矩阵：$A$ 和 $B$ 相似，即存在 $P^{-1}AP=B$，那么 $\parallel A\parallel =\parallel B\parallel$。

  

  • ${\alpha }_1,{\alpha }_2,{\alpha }_3$ 线性无关，即 $({\alpha }_1,{\alpha }_2,{\alpha }_3)$ 是满秩可逆矩阵。
  • 利用 $A({\alpha }_1,{\alpha }_2,{\alpha }_3)=({\alpha }_1,{\alpha }_2,{\alpha }_3)B$ 可以得到 $A$ 和 $B$ 相似，其中 $B$ 由题给条件得出。则 $\parallel A\parallel =\parallel B\parallel$。

1.4. 求 (代数) 余子式的线性组合

• 题型：已知 $\parallel A\parallel$，要求 A 其中某些（代数）余子式的线性组合。

• 原理：$A_{ij}$ 和 $a_{ij}$ 无关，所以可以直接将系数替换 $a_{ij}$，求新的行列式。

• 注意：代数余子式已经包含 $(-1{)}^{i+j}$ 项，替换时无需考虑正负，直接代入！！

• 例

  

  • 分别求每行的代数余子式之和，然后再相加。
  • 求第 $i\ge 2$ 行的余子式之和会将第 $i$ 行全部换成 1，此时和第 1 行成比例直接为 0.
  • 也可以利用 $A^{\ast }$ 是由 $A$ 的全部代数余子式构成，求 $A^{\ast }$，再求和。

2. 秩为 1 矩阵

2.1. 性质

• $r(A)=1$，$A$ 的任意两行两列都成比例。
• $A$ 可以写成 $A=\alpha {\beta }^T$，其中 $\alpha ,\beta$ 都是 $n\times 1$ 列向量。
• $\mathrm{tr}(A)=a_{11}{b}_{11}+a_{22}{b}_{22}+a_{33}{b}_{33}={\beta }^T\alpha$，即 $A$ 的迹和向量内积相等。
• $A$ 特征值为 $\mathrm{tr}(A)$ 和 0，$\mathrm{tr}(A)\ne 0$ 时占 1 重，0 占 $n-1$ 重；$\mathrm{tr}(A)=0$ 时，0 占全部 $n$ 重。
  • $A$ 对应 $\mathrm{tr}(A)$ 的特征向量为 $k\alpha$，$k=\mathrm{const}$。

2.2 特征值证明

• $\lambda =\mathrm{tr}(A)$：用 $A\alpha =(\alpha {\beta }^T)\alpha =({\beta }^T\alpha )\alpha =\mathrm{tr}(A)\alpha$；
• $\lambda =0$：用线性方程组性质
  • 构造 $Ax=0$，因为 $r(A)=1$，方程有 $n-1$ 个线性无关的基础解向量。
  • 即 $Ax=0x$ 有 $n-1$ 个线性无关的特征向量。0 至少为 $n-1$ 重特征值。

2.3. 题型

• 求幂：展开为 $A=\alpha {\beta }^T$，中间 ${\beta }^T\alpha$ 化成常数 $\mathrm{tr}(A)$。$A^n={\mathrm{tr}}^{n-1}(A)A$；
• 求特征值：2.1 性质；
• 相似：因为 2.1 性质，当 $\mathrm{tr}(A)\ne 0$ 时，必有 $P$ 使得 $P^{-1}AP=\mathrm{\Lambda }$，即 $A$ 可相似对角化为 $\mathrm{\Lambda }$。

3. 初等变换

3.1. 高斯—若尔当消元

将一个矩阵 $A$ 和另一个矩阵 $B$ 在行方向上增广，拼成 $C=(A\parallel B)$，那么对 $C$ 做初等行变换，等价于同时对 $A$ 和 $B$ 做初等行变换。

将一个矩阵 $A$ 和另一个矩阵 $B$ 在列方向上增广，拼成 $C=\left(\begin{array}{c}A\\ B\end{array}\right)$，那么对 $C$ 做初等列变换，等价于同时对 $A$ 和 $B$ 做初等列变换。

• 用途 1：求逆
  • 将 $A$ 和 $E$ 行拼接后，对 $A$ 进行行变换得到行最简型 $B$，此时 $E$ 变为 $E^{\prime }$。若 $B=E$ 则 $A^{-1}=E^{\prime }$。
  • $B$ 和 $E^{\prime }$ 列拼接后，对 $B$ 做列变换化为 $E$，$E^{\prime }$ 随之化为 $E^{″}$，则 $A^{-1}=E^{″}$。
• 用途 2：记录初等变换矩阵。即求初等变换矩阵 $P,Q$ 使得 $PAQ=B$。做法同 1，选 $E$ 来拼即可。
• 用途 3：解非齐次线性方程组，本质同 1 和 2，增广一列非零向量，所以只能做行变换。